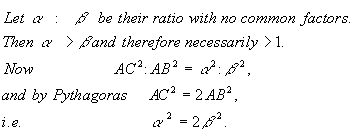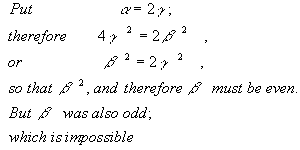| |
Return to MENU
Back
PYTHAGORAS
of
SAMOS
A Collection of Essays and Lessons for Junior and Senior High School
Contents
6. Early concepts of Number and Number Mysticism
7. Figurate Numbers
8. Number Patterns in Music
9. Incommensurables
10. Academic
Introduction:
The Pythagorean view of the universe rested squarely on the belief that Natural (counting) number was the key to the various qualities of mankind and matter. Since in their view everything was composed of number, the explanation for an objects existence could only be found in number. Elsewhere about this time, number existed for utilitarian purposes only, as a device for solving problems in calendar construction, building and commerce. It was the Pythagoreans who saw number as important in itself, the numbers themselves having "personality in a rustic landscape".
The distinction was made between logistic (art of computation) and arithmetic (number theory). Kline [6 ] quotes the famous Pythagorean Philolaus (425 B.C.E.), as writing:
"Were it not for number and its nature, nothing that exists would be clear to anybody either in itself or in its relation to other things...You can observe the power of number exercising itself ... in all acts and the thoughts of men, in all handicrafts and music."
Pythagoras and the early Order initially treated number concretely, as patterns with pebbles, but over time the Pythagoreans developed and refined their concept of number into the same abstract entity which still exists today. Though it is difficult to separate fact from fancy in some of the surviving references to the Pythagoreans, it is generally conceded that they began number theory, and were responsible for the introduction and development of number mysticism in Western Society.
A. Early concepts of Number and Number Mysticism
Number mysticism is not generally associated with "serious mathematics" but from the early Pythagoreans until the 19th century many venerated mathematicians practised some forms of numerology. In more recent times this was in return for patronage from the influential and aristocratic circles who sought some mystical assistance in their daily endeavours. Even today, existing Western cults refer to Pythagorean doctrines on number. According to Boyer [7]:
"Many early civilisations shared various aspects of numerology, but the Pythagoreans carried number worship to its extreme, basing their philosophy and their way of life upon it."
To the Pythagoreans, each number possessed its own special attributes. See for example the table below.
| Number | Property of the number |
| | |
| 1 | monad(unity) generator of numbers, the number of reason |
| 2 | dyad(diversity, opinion) first true female number |
| 3 | triad(harmony = unity + diversity) first true male number |
| 4 | (justice, retribution) squaring of accounts |
| 5 | (marriage) = first female + first male |
| 6 | (creation) = first female + first male + 1 ? |
| 10 | (Universe) tetractys |
Fortunately, in developing their number mysticism, the Pythagoreans also valued rigour and proof. To this end they searched for the essential properties and definitions of many numbers. The following is a brief description of their ideas about number.
- Definitions of Unity
Some of the early definitions of unity are found in Heath [9] where the monad is described as "limiting quantity", or as "the common part or beginning of how many".
- Definitions for Number
Similarly, there were many different definitions for number, the Pythagorean being essentially: "Number is a collection of units"
- Definitions for Odd/Even Numbers
The Pythagoreans made the distinction between odd and even numbers as seen in this early definition (Iamblichus in Heath):
"An even number is that which admits of being divided, by one and the same operation, into the greatest and the least (parts), greatest in size but least in quantity (i.e. two lots each half size) ... while an odd number is that which cannot be so treated, but is divided into two unequal parts"
Many superstitions became associated with the odd and even numbers. For example the odds were considered masculine and divine while the evens were considered feminine and thus earthly and human. It is interesting to note here that due to the influence of Pythagoras, the Pythagoreans (against contemporary practice) welcomed women into the Order, and that Pythagoras' wife, Theano was considered an accomplished mathematician in her time. It is thought that Theano and two of her daughters to Pythagoras carried on his work after his death.
- Definitions for Prime/CompositeNumber
Early Pythagoreans described what we would call prime numbers as "prime and incomposite numbers" and it was generally accepted that a prime number was "measured by no number, but by an unit only", though there was some disagreement about whether 2 was prime. The composite numbers were those which were "measured by any less number". In keeping with the early Pythagorean view of number as a pattern of stones, prime numbers were also called rectilinear because they can be represented as a line of stones only, compared to the composites which can also be arranged into equal size groups of stones. Composites were further distinguished as plane or solid. Heath quotes Theon of Smyrna (1st century A.D) as writing:
"of composite numbers they call those which are contained by two numbers plane, as being investigated in two dimensions and, as it were, contained by a length and a breadth, while (they call) those (which are contained) by three (numbers) solid, as having the third dimension added to them."
You might like to do Activity 3 before you continue.
- The Tetractys
To the Pythagoreans the holiest number of all was the number 10 or the tetractys. In addition to their other "personalities" the first four numbers had a special significance in that their sum accounted for all the possible dimensions:
| Number | Geometric property | Geometric shape |
| 1 |
generator of dimension
|  |
| 2 |
line of dimension 1
|  |
| 3 | triangle of dimension 2 |  |
| 4 | tetrahedron of dimension 3 | 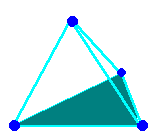 |
Summing these we get 1+2+3+4 = 10
Since these were the only numbers that were needed to demonstrate all known objects (geometrically) then the sum of all these objects, that is the sum of these numbers, was believed to represent the known Universe. The properties of the tetractys still have persuasive influence in mystic cults of today. Some argue that it was the Pythagorean veneration of the tetractys, not so much the number of digits on hands or feet, which is responsible for our present use of the base ten.
In addition to the tetractys, the Pythagoreans developed other concepts of "fourness" in nature such as the material elements of earth, air, fire, and water.
For more on the mystic properties of number see the essays on the Pythagorean Pentagon by John Opsopaus at the University of Tennessee.
- A Model for the Universe
Since the tetractys was the number for the Universe, the Pythagoreans believed that there had to be 10 heavenly bodies. In addition to the visible earth, sun, moon and five planets, they added a central fire and a "counter-earth" on the opposite side of the central fire. This initial attempt at explaining cosmology in terms of mathematical principles is the foundation of our present models for the Universe. Burnet[10] claims:
"It is probable, at any rate, that this theory started the train of thought which made it possible for Aristarchus of Samos to reach the heliocentric hypothesis, and it was certainly Aristotle's successful reassertion of the geocentric theory which made it necessary for Copernicus to discover the truth afresh. We have his own word for it that he started from what he had read about the Pythagoreans."
- Definitions for Amicable Numbers
The Pythagoreans, on Iamblichus' (in Heath) somewhat doubtful authority, are credited with discovering amicable numbers. Two numbers are amicable if each is the sum of the proper divisors (that is all the divisors except the number itself) of the other.
For example 220 and 284 are amicable since the sum of the proper divisors of 220 are 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284 and the sum of the proper divisors of 284 are 1 + 2 + 4 + 71 + 142 = 220. Superstition maintained that two talismans bearing this pair of numbers would seal a perfect friendship between the wearers. The pair also became significant in magic, sorcery, and astrology.
- Definitions for Deficient/Perfect/Abundant Numbers
Other numbers which were given mystical powers and were associated with the Pythagoreans were the perfect, deficient, and abundant numbers.
A number is perfect if it is equal to the sum of its proper divisors, is deficient if its sum falls short of the number, and is abundant if the sum exceeds the number. 6 is a perfect number (1 + 2 + 3), 8 is deficient (1 + 2 + 4), and 12 is abundant (1 + 2 + 3 + 4 + 6).
B Figurate Numbers
To Pythagoras and the early Pythagoreans, number was "atomistic", it existed as bundles of a fundamental elementary object - unity. Numbers were represented as patterns formed by collections of these units. These form the so-called figurate or polygonal numbers, the triangular, square, pentagonal, oblong, etc. In fact when we call numbers "figures" today we are using the jargon of the Pythagorean Order. We have already looked at some of the properties of the square numbers in an earlier essay.
Most figurate numbers begin with the number generator 1. From there the next number is determined by the the number of pebbles needed to make the desired pattern:
| Figurate Number | Geometric shape |
| triangular numbers | 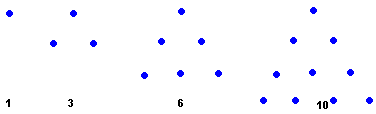 |
| square numbers | 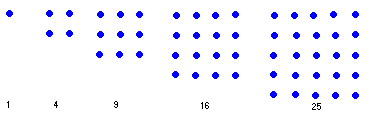 |
| pentagonal numbers | 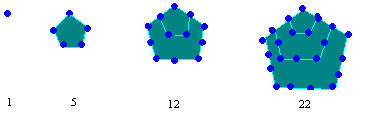 |
| oblong numbers | 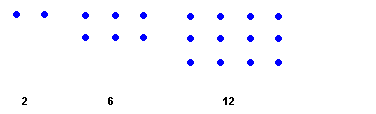 |
The Oblong numbers are those that can be arranged in a rectangle one unit wider than it is high; each is twice a
Triangular number. The Oblongs have sides in the ratios 1:2, 2:3, 3:4, 4:5, 5:6,....
You might like to do Activity 4 before you continue.
C. Number Patterns in Music
Readers who are familiar with the theory of music will recognise the list of oblongs above as the intervals in decreasing order of consonance: Octave,Perfect Fifth, Perfect Fourth, Major Third (4:5), Minor Third (5:6), etc. It is Pythagoras who is credited with discovering this mathematical relationship between music and number.
This discovery, that the pitch of a note is related to the length of the string which produced it, is credited as being the spark which ignited Pythagoras' imagination and philosophy. It allowed Pythagoras a glimpse of a whole new order in the Universe, one governed by intellect and logic and capable of the sublimest of pleasures. And a glimpse was all that he needed. With this discovery, Pythagoras and the Pythagoreans set in train a way of investigation which has proved to be one of the most productive ideas in human history - that mathematics can be used to unravel the mysteries of the Universe. It was, in the words of Koestler [8] :
"..epoc-making: it was the first successful reduction of quality to quantity, the first step towards the mathematization of human experience - and therefore the begining of science..."
The Music of the Spheres
The Pythagoreans wove their musical discoveries into their mathematical cosmology to produce a hauntingly beautiful description of the Universe. The Pythagorean Universe consisted of a central, spherical earth surrounded by the heavenly objects. These were attached to crystal spheres at distances determined by the regular solids (solids which can be circumscribed by a sphere). The rotation of these spheres produced wondrous musical harmonies. The Pythagoreans explained that normal people can not hear the "harmony of the spheres" because they have grown too accustomed to hearing it from birth (Pythagoras alone was supposed to be able to hear it). Nonetheless the quest for the mathematics behind these harmonies captivated some of the greatest minds over the next two thousand years.
Koestler describes how the early physicist Kepler spent much of his productive life trying to discover the harmony of the spheres. The three laws he is best remembered for were virtually footnotes to his investigations into the harmonies.
D Incommensurables
The early Pythagorean belief that "all was (Natural) number" meant that they did not consider fractions as numbers. What we consider as fractions today were seen by the early Pythagoreans as ratios of Natural numbers as in the musical scales above, not as numbers in their own right. It was fundamental to the beliefs of the early Pythagoreans that all things (abstract, natural, human affairs) were understandable by considering the intrinsic properties of Natural numbers and their ratios. This was the foundation of the faith and scholarship of Pythagoras and essential to this faith was the concept of commensurability. Heath quotes the first scholium on Book X of the Elements as stating:
"..the Pythagoreans were the first to address themselves to the investigation of commensurability, having discovered it by means of their observation of numbers...They called all magnitudes measurable by the same measure commensurable"
For example, the number 8 can be measured in twos - the rectangular number 4 x 2, 12 can be also measured in twos - the rectangular number 6 x 2, so 8 and 12 are commensurable as they both can be measured in twos . Similarly with geometry, they reasoned that given any two line segments of unequal length, it should always be possible to find a third line segment, perhaps very small, that can be marked off a whole number of times into each of the given segments. With the concept of commensurability, the early Pythagoreans could confidently base their faith on "all is number". If any pair of numbers were found to be incommensurable then the philosophical foundation of the Order would be threatened. It is generally accepted that such a threat did eventuate in Pythagoras' time and that it arose in the investigation of the cherished Pythagorean Theorem.
The discovery which created such a threat to Pythagoreanism was that natural numbers or their ratio are not sufficient when comparing the length of the diagonal of a square to its side. It is not possible to find a Natural number which measures both the diagonal and the side of a square. Similarly it is not possible to find a small length which can be marked off a whole number of times into both the diagonal and the side. The belief that all the secrets of the Universe would be found in Natural numbers was in tatters. There existed, contrary to intuition, incommensurable numbers and line segments. We call the numbers needed to represent the length of the diagonal, the irrational numbers meaning - "unable to be expressed as a ratio".
The early Pythagoreans have been credited with the discovery of the irrational number 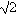 , though it is not clear whether they had expanded their investigations into any other surds. Certainly within the next couple of centuries many of the smaller surds were identified. The discovery of the irrationals and the philosophical difficulties it created in number theory diverted Greek mathematics to the rigours of geometry where the measure of incommensurables was less troublesome - they could represent a line of length , though it is not clear whether they had expanded their investigations into any other surds. Certainly within the next couple of centuries many of the smaller surds were identified. The discovery of the irrationals and the philosophical difficulties it created in number theory diverted Greek mathematics to the rigours of geometry where the measure of incommensurables was less troublesome - they could represent a line of length 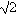 even if they couldn't measure it, simply by drawing the diagonal of a unit square. Heath claims: even if they couldn't measure it, simply by drawing the diagonal of a unit square. Heath claims:
"...it was inevitable that the Pythagoreans should investigate the relations between sides and hypotenuse of other right-angled triangles. They would naturally give special attention to to the isosceles right-angled triangle; they would try to measure the diagonal, would arrive at successive approximations, in rational fractions, to the value of 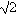 , and would find that successive efforts to obtain an exact expression for it failed. It was however an enormous step to conclude that such exact expression was impossible, and it was this step which the Pythagoreans made. ... The actual method by which the Pythagoreans proved the incommensurability of , and would find that successive efforts to obtain an exact expression for it failed. It was however an enormous step to conclude that such exact expression was impossible, and it was this step which the Pythagoreans made. ... The actual method by which the Pythagoreans proved the incommensurability of 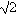 with unity, was no doubt that referred to by Aristotle, (...) a reductio ad absurdum by which it is proved that, if the diagonal is commensurable with the side, it will follow that the same number is both odd and even." with unity, was no doubt that referred to by Aristotle, (...) a reductio ad absurdum by which it is proved that, if the diagonal is commensurable with the side, it will follow that the same number is both odd and even."
The Pythagorean proof is still as elegant and breathtaking in its logical structure today as it was then. The proof "reductio ad absurdum" is also called " Proof by Contradiction"; that is, we assume that there is a fraction in lowest terms whose square is 2, and we will logically deduce from this that the fraction is even and simultaneously is odd. This obvious fallacy means that we are then forced to reject the proposition that there is a fraction whose square is 2. The Pythagorean proof (in modern language) is thought to have gone like this:
Suppose AC, the diagonal of a square, to be commensurable with AB, its side.
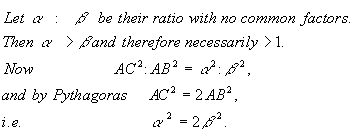

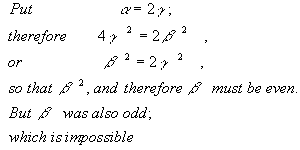
Therefore the original supposition that the diagonal of a square is commensurable with its side is not possible. So incommensurable or irrational numbers exist. | 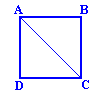 |
If, as has been asserted, the two discoveries of The Theorem and the presence of number patterns in music started the Pythagoreans along the road to science, surely the discovery of this simply elegant and beautiful proof must have convinced them that they were on the right road.
On to Pythagorean Algebra
References:
[6] Kline, Morris B.,Mathematics- The Loss of Certainty, N.Y.:Oxford University Press, 1980
[7] Boyer, Carl B., A History of Mathematics, N.Y.: John Wiley and Sons, 1968
[8] Koestler, Arthur, The Sleepwalkers - A History of Man's Changing Vision of the Universe. London: Hutchinson & Co., 1959
[9] Heath, Sir Thomas L., Euclid - The Thirteen Books of The Elements Second Edition Vol i, N.Y.: Dover Publications (orig 1908) On-line version with java applet
[10] Burnet, John, Early Greek Philosophy, 3rd Ed., London: Adam and Charles Black, 1920.
[11] This Essay and the related classroom Activities are on-line at MATHGYM ( http://www.mathtrak.com.au/mic/ )
|
![]()
![]()






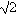 , though it is not clear whether they had expanded their investigations into any other surds. Certainly within the next couple of centuries many of the smaller surds were identified. The discovery of the irrationals and the philosophical difficulties it created in number theory diverted Greek mathematics to the rigours of geometry where the measure of incommensurables was less troublesome - they could represent a line of length
, though it is not clear whether they had expanded their investigations into any other surds. Certainly within the next couple of centuries many of the smaller surds were identified. The discovery of the irrationals and the philosophical difficulties it created in number theory diverted Greek mathematics to the rigours of geometry where the measure of incommensurables was less troublesome - they could represent a line of length 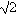 even if they couldn't measure it, simply by drawing the diagonal of a unit square. Heath claims:
even if they couldn't measure it, simply by drawing the diagonal of a unit square. Heath claims:
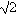 , and would find that successive efforts to obtain an exact expression for it failed. It was however an enormous step to conclude that such exact expression was impossible, and it was this step which the Pythagoreans made. ... The actual method by which the Pythagoreans proved the incommensurability of
, and would find that successive efforts to obtain an exact expression for it failed. It was however an enormous step to conclude that such exact expression was impossible, and it was this step which the Pythagoreans made. ... The actual method by which the Pythagoreans proved the incommensurability of 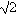 with unity, was no doubt that referred to by Aristotle, (...) a reductio ad absurdum by which it is proved that, if the diagonal is commensurable with the side, it will follow that the same number is both odd and even."
with unity, was no doubt that referred to by Aristotle, (...) a reductio ad absurdum by which it is proved that, if the diagonal is commensurable with the side, it will follow that the same number is both odd and even."