Return to MENU
Back

Activity 3 - Odds and Evens and Direct Proof

 This Activity and the related Essay on Pythagorean Number are on-line at MATHGYM ( http://www.mathtrak.com.au/mic/ )

In this activity I will attempt to describe how the Pythagoreans may have arrived at some of their understandings about number. Along the way I hope to give you some additional insight into the way that Mathematicians work, and how they can be confident that their discoveries are right.
A USEFUL LAW

Before we get into our investigations of odd and even numbers we need to learn a law that the Pythagoreans first discovered. The law is called the Distributive Law and is written as:

a(b+c) = ab + ac and its converse ab + ac = a(b+c).
The Pythagoreans demonstrated this Law using the area of a rectangle of width a and length b+c, as in the diagram below:
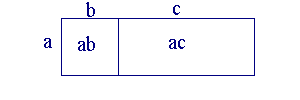
Can you see how the Law is demonstrated? The large rectangle is divided up into two smaller rectangles of size a by b and a by c respectively. The area of a rectangle is length times breadth. So the area of the large rectangle is a times (b + c). But the area of the larger rectangle is the sum of the areas of the two smaller ones or ab plus ac. So ab + ac = a(b+c).

DEFINITIONS OF ODDS AND EVENS

In this Activity, we will be talking only about positive whole numbers and investigate some of the properties of odd and even numbers, something the Pythagoreans were very fond of. The early Pythagoreans visualised number as a collection of pebbles. In the accompanying essay we looked at how they identified numbers by the patterns they produced - triangular, square, pentagonal etc. They distinguished between odd and even numbers by recognising the different way that these numbers could be grouped. I will repeat what was said in the essay here:

"An even number is that which admits of being divided, by one and the same operation, into the greatest and the least (parts), greatest in size but least in quantity (i.e. two lots each half size) ... while an odd number is that which cannot be so treated, but is divided into two unequal parts"

In modern language, the Pythagoreans were saying: "Given any even number of pebbles, we can always assemble the pebbles into two equal groups, but any odd number of pebbles cannot be so grouped."

Definition of Even Numbers
In the diagram below an even number is separated into two equal groups. The "..." means "and so on" or "continue this pattern". By putting the "..." there we have allowed our diagram to represent any even number - all you need to do to represent a given even number is fill in the necessary pairs of dots for the "...".

An algebraic way that we can define even numbers is to say: "An even number is divisible by 2, and therefore it can always be written as 2 times some other number. If we let that "other number" be "n" then we can write any even number as 2n.

Definition of Odd Numbers
If we now arrange any odd number of pebbles into two groups we will always have two uneven groups, and the closest we can get to equal groups will always have one group with one extra pebble.

The algebraic definition for odd numbers is: "When we divide an odd number by 2, there will always be a remainder of one. Therefore an odd number is always equal to 2 times some other number, plus one or 2n+1.

PROPERTIES OF ODDS AND EVENS

What do you think you will get if you add an even number and another even number - an even or an odd number? If I didn't know the answer to this I might start with actual even numbers and try a few additions. Here is the beginning of my investigation:

2 + 4 = 6
6 + 10 = 16
4 + 8 = 12
After a while I notice that the answer is always an even number. At this stage I am ready to make a conjecture. Here it is:

Conjecture - [1] Even plus even is even

Have I proven the conjecture? No I haven't because the next pair of evens I investigate might add to be odd!! My conjecture implies that all evens will add to give an even. How can I possibly investigate all evens! Obviously I can't. This is where Pythagoras showed his genius. He realised that to be confident that a statement was in fact true it had to be logically proven - and proofs always start with the definitions that were used. Here is a geometric proof of my conjecture. I use the geometric definition of even numbers to show that the result of the addition of two evens is by definition another even as shown below:

What the geometric proof shows is: "when you add two equal rows of pebbles to another two equal rows of pebbles you will always get two equal rows of pebbles."

We can prove this using our algebraic definitions. Here is the algebraic proof:

Let the two even numbers be x and y.
Now by definition let x= 2n and y = 2m
Therefore x+y= 2n + 2m

 = 2 (n+m) - by the distributive law
 = 2p where p is any number equal to n+m
 Which, by definition is an even number.

Question 1:

See if you can prove the Conjecture - [2] Even minus even is even by both geometric and algebraic methods

Question 1 - Answer


Question 2:

See if you can prove the Conjecture - [3] Odd plus odd is even by both geometric and algebraic methods

Question 2 - Answer


Question 3:

See if you can prove the Conjecture - [4] Odd minus odd is even by both geometric and algebraic methods

Question 3 - Answer


Question 4:

See if you can prove the Conjecture - [5] Even plus odd is odd by both geometric and algebraic methods

Question 4 - Answer


Question 5:

See if you can prove the Conjecture - [6] Even minus odd is odd by both geometric and algebraic methods

Question 5 - Answer

Next, let's see what happens when we multiply.

I will start once again with actual even numbers and try a few multiplications. Here is the beginning of my investigation:

2 x 4 = 8
6 x 10 = 60
4 x 8 = 32
After a while I notice that the answer is always an even number. At this stage I am ready to make a conjecture. Here it is:

Conjecture - (7) An even number times an even number is even

This conjecture can be proven using the geometric method but at this stage we should be confident enough to use the algebraic method. Here is the algebraic proof:

Let the two even numbers be x and y
Therefore, by definition, let x = 2n and y = 2m
so   x X y = 2n X 2m

= 2 (2nm)
= 2 p where p is a number equal to 2nm
 Which is, by definition even.


Question 6:

See if you can prove the Conjecture - [8] The square of an Even number is even by algebraic methods.

Question 6 - Answer


Question 7:

Can you prove the converse of this. The converse means the reverse of the statement. That is :
Conjecture - [9] If n2 is even than n is even by algebraic methods.

Question 7 - Answer


Question 8:

See if you can prove the Conjecture - [10] Odd times odd is odd by algebraic methods.

Question 8 - Answer


Question 9:

See if you can prove the Conjecture - [11] Even times odd is even by algebraic methods.

Question 9 - Answer

 

Answer Question 1

Here is the geometric proof:

Here is the algebraic proof:

Let the two even numbers be x and y.
Now by definition let x= 2n and y = 2m
Therefore x-y= 2n - 2m

 = 2 (n-m) - by the distributive law
 = 2p where p is any number equal to n+m
 Which, by definition is an even number.

Back

 

Answer Question 2

Here is the geometric proof:

Here is the algebraic proof:

Let the two odd numbers be x and y.
Now by definition let x= 2n + 1 and y = 2m + 1
Therefore x+y= (2n + 1) + (2m+1)

 = 2n+2m + 2
 = 2(n + m + 1)by the distributive law
 = 2p where p is any number equal to n+m+1
 Which, by definition is an even number.

Back

 

Answer Question 3

Here is the geometric proof:

Here is the algebraic proof:

Let the two odd numbers be x and y.
Now by definition let x= 2n + 1 and y = 2m + 1
Therefore x-y= (2n + 1) - (2m+1)

 = 2n-2m
 = 2(n - m)by the distributive law
 = 2p where p is any number equal to n-m
 Which, by definition is an even number.


Back

 

Answer Question 4

Here is the geometric proof:

Here is the algebraic proof:

Let the even number be x and the odd number be y.
Now by definition let x= 2n and y = 2m + 1
Therefore x+y= 2n + (2m+1)

 = 2n+2m+1
 = 2(n + m) + 1by the distributive law
 = 2p + 1 where p is a number equal to n+m
 Which, by definition is an odd number.

Back

 

Answer Question 5

Here is the geometric proof:

Here is the algebraic proof:

Let the even number be x and the odd number be y.
Now by definition let x= 2n and y = 2m + 1
Therefore x-y= 2n - (2m+1)

 = 2n-2m - 1
 = 2(n - m) - 1by the distributive law
 = 2p - 1where p is a number equal to n-m
 Which, by definition is an odd number.

Back

 

Answer Question 6

Here is the algebraic proof:

Let the even number be x
Therefore, by definition, let x = 2n
so   x2 = 2n X 2n

= 2 (2n2)
= 2 p where p is a number equal to 2n2
 Which is, by definition even.

Back

 

Answer Question 7

Here is the algebraic proof:

Since n2 is even it must have a factor of 2. But the factors of perfect squares must come in at least pairs. So each factor n must have a factor of at least one 2.
Therefore n is by definition even.

Back

 

Answer Question 8

Here is the algebraic proof:

Let the two odd numbers be x and y.
Now by definition let x= 2n + 1 and y = 2m + 1
Therefore x X y= (2n + 1)(2m+1)

 = 2n(2m+1) + 1(2m+1)by the distributive law
 = 4nm+2n+2m+1by the distributive law
 = 2(2nm+n+m)+1also by the distributive law
 = 2p+1where p is a number equal to 2nm+n+m
 Which, by definition is an odd number.

Back

 

Answer Question 9

Here is the algebraic proof:

Let the even number be x and the odd number be y.
Now by definition let x= 2n and y = 2m + 1
Therefore x X y= 2n(2m+1)

 = 4nm+2n by the distributive law
 = 2(2nm+n) by the distributive law
 = 2p where p is a number equal to 2nm+n
 Which, by definition is an even number.

Back