Back
A Collection of Essays and Lessons for Junior and Senior High School
This confidence in the "tangibility" and rigour of geometry lasted through to the 17 century. Sir Isaac Newton is considered to be influential in the acceptance of algebraic procedures, though he would not publish his monumental "The Mathematical Principles of Natural Philosophy" until he had established the geometric proofs to replace his algebra and calculus. Kline[11] states:
"In The Principles he [Newton] used geometric methods and he gave theorems on limits in geometric form. He admitted much later that he used analysis to find the theorems in The Principles, but he formulated the proofs geometrically to make the arguments as secure as those of the ancients."
It is important that I restate what I have said before; that it is impossible to know for certain which of the following is the result of Pythagoras and which is the work of later Pythagoreans or even later Mathematicians. All of the following ideas come from the early Books of The Elements[12]. It is generally, but not universally, agreed that the ideas in these Books are essentially Pythagorean in origin. It is very tempting to give this essay a rigorous treatment as developed in The Elements, but I will leave interested readers to pursue such a treatment in the references below. The purpose of this essay is to give the reader an appreciation of the development of Greek algebra in as much as it was geometric in nature.
As explained above the early Greek mathematicians resorted to geometry to rigorously prove (and demonstrate) their ideas. It is unclear what their initial tools were but by the time of Euclid[12] all constructions were to be done by straightedge and compass, so it is useful to digress for a moment to describe these tools. A straightedge is essentially an idealised ruler with the difference that it is unlimited in length and has no scale markings. It is not a measuring tool but a construction tool, allowing the user to produce a straight line of any length. The compass of The Elements is similar to the one used today with one very important distinction. The Classical compass collapses after use. By this I mean that you can open the compass to draw an arc but once that arc is drawn the compass collapses so that the size of the arc is not preserved between applications. This feature of the Classical compass renders some common constructions (easily taught in school using the "preserving" compass) somewhat non-trivial.
Addition and Subtraction
To place at a given point (as an extremity) a straight line equal to a given straight line
This construction is described in Heath[12] as below:
We can now consider Proposition 3. Though specifically used for subtraction of lengths, it could also be used to add two lengths. This Proposition states
Given two unequal straight lines, to cut off from the greater a straight line equal to the less.
To add C to BA one has simply to extend BA and consider the sum to be where the circle DEF intersects with BA extended.
Multiplication
Division
This is the so-called "application of areas". This example is a specific case of Proposition I. 44. Of this Proposition Heath claims:
"This proposition will always remain one of the most impressive in all geometry... The marvellous ingenuity of the solution is indeed worthy of the "godlike men of old" as Proclus calls the discoverers of the method of "application of areas"; and there would seem to be no reason to doubt that the particular solution, like the whole theory, was Pythagorean..."
The Pythagoreans also used geometric proportion to perform division. This is discussed in Section C below.
The addition or subtraction of products is, in geometric algebra, the addition and subtraction of areas of rectangles and squares, the answer being transformed into a single rectangle by the application of areas to any line of any length. To find a square root the Pythagoreans would use a construction that converted a rectangle into a square of equivalent area.
Proposition 1. If there be two straight lines, and one of them be cut into any number of segments whatever, the rectangle contained by the two straight lines is equal to the rectangles contained by the uncut straight line and each of the segments.
In algebraic form this is written as: a(b+c+d+...) = ab+ac+ad+.... This Proposition is what today we call the Distributive Law and in its simplest form is written as:
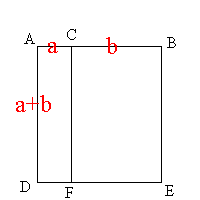
Proposition 2. If a straight line be cut at random, the rectangle contained by the whole and both of the segments is equal to the square on the whole.
In algebraic form this is written as: (a+b)a + (a+b)b = (a+b)2. This is easily seen with a construction as shown. The line AB is cut at random at C. A rectangle is constructed on AC and AB so that the length of AD, CF and BE are equal to AB. This makes the square ABED. If we let AC be a and CB be b then AB and AD equal (a+b) in length. So the area of the square is (a+b)2, and the area of each rectangle is (a+b)a and (a+b)b. It remains to notice that the square is formed as the sum of the two rectangles.
This is essentially the Distributive Law in that (a+b)a = a2 + ab. I leave it to the reader to prove it from the construction opposite.
This is the binomial expansion (a+b)2 = a2 + 2ab + b2. I leave it to the reader to prove it from the construction opposite.
Eves[13] states:
"In their geometric algebra, the Greeks employed two principal methods for solving certain simple equations - the method of proportions and the method of application of areas. There is evidence that both of these methods originated with the Pythagoreans".
The Pythagoreans identified many different "styles" of quadratics, and applied their geometrical propositions to each different style to arrive at a unque solution for each. This essay will only show a few of their techniques; the interested reader should look in Books II and VI of The Elements for a more comprehensive treatment.
Solving Equations by Proportion
For example, if they wished to solve 4x = 2 x 32, they would construct a straight line ABC 36 units long with B 4 units from A. At an angle to AC, a second segment AED would be drawn with E placed at a distance of 2 units from A. EB would be joined and CD constructed parallel to BE. The resulting segment ED would represent the solution to the equation (16 units).
For example, to solve x2 = 8 x 2, they would construct a semicircle with diameter AB 10 units in length and with AC 8 units. The length of the perpendicular from C to the circumference of the semicircle (CD) is the solution of the equation (4 units).
"These things says Eudemus, are ancient and are discoveries of the Muse of the Pythagoreans, I mean the application of areas, their exceeding and their falling short."
Proposition 5 of Book II of The Elements states:
If a straight line be cut into equal and unequal segments, the rectangle contained by the unequal segments of the whole together with the square on the straight line between the points of section is equal to the square on the half.
Draw AB equal in length to a . Bisect AB at C. Draw CO perpendicular to AB and equal in length to b. Produce OC to N so that ON is equal in length to CB (a/2). With O as centre and radius ON, describe a circle cutting CB in D.
This is because triangle CDO is right-angled with CO (= b), OD (= a/2), and CD (= a/2-x) being Pythagorean triples. Thus
Though the justification for this construction may require some understanding, the construction itself is quite straight forward. Of course for a Real solution to this style of quadratic, b2 must not be greater than (a/2)2.
This essay has attempted to demonstrate how the early Pythagoreans were able to use their discoveries of proportion and geometry to solve linear and quadratic equations. In this way they were able to perform algebraic processes similar to those expected of Junior High school students today; a degree of sophistication not often credited to them.
[11] Kline, Morris B.,Mathematics- The Loss of Certainty, N.Y.:Oxford University Press, 1980
[12] Heath, Sir Thomas L., Euclid - The Thirteen Books of The Elements Second Edition Vol i, N.Y.: Dover Publications (orig 1908) On-line version with java applet
[13] Eves, Howard, An Introduction To The History of Mathematics 5th Ed., N.Y.: Saunders College Publishing, 1983
Contents
10. A. Geometric basis for arithmetic operations
11. B. Algebraic identities
12. C. Solving Equations
13. D. Academic
Introduction:
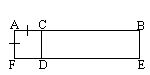
The early Definitions, Postulates, Common Notions , and Propositions of Book I in The Elements account for these constructions. Without repeating these I will show how addition and subtraction were constructed. Firstly Proposition 1, Book I of The Elements shows how to construct an equilateral triangle. Armed with this, Proposition 2 shows how 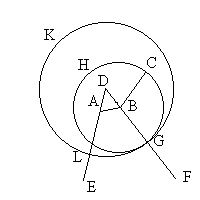 Let A be the given point, and BC the given straight line. Thus it is required to place at point A (as an extremity) a straight line equal to the straight line BC.
Let A be the given point, and BC the given straight line. Thus it is required to place at point A (as an extremity) a straight line equal to the straight line BC.
From the point A to the point B let the straight line AB be joined; and on it let the equilateral triangle DAB be constructed.
Let the straight lines AE, BF be produced in a straight line with DA, DB; with centre B and distance BC let the circle CGH be described; and again with centre D and distance DG let the circle GKL be described.
Then, since the point B is the centre of the circle CGH, BC is equal to BG.
Again, since the point D is the centre of the circle GKL, DL is equal to DG.
And in these DA is equal to DB; therefore the remainder AL is equal to the remainder BG.
But BC was also proved equal to BG; therefore each of the straight lines AL, BC is equal to BG.
And things which are equal to the same thing are also equal to one other; therefore AL is also equal to BC.
Therefore at the given point A the straight line AL is placed equal to the given straight line BC.
(Being) what it was required to do.
 Let AB, C be the two given unequal straight lines and let AB be the greater of them.
Let AB, C be the two given unequal straight lines and let AB be the greater of them.
Thus it is required to cut off from AB the greater a straight line equal to C the less.
At the point A let AD be placed equal to the straight line C (Proposition I. 2 above); and with centre A and distance AD let the circle DEF be described.
Now, since the point A is the centre of the circle DEF, AE is equal to AD.
But C is also equal to AD.
Therefore each of the straight lines AE, C is equal to AD; so that Ae is also equal to C.
Therefore, given the two straight lines AB, C, from AB the greater AE has been cut off equal to C the less.
(Being) what it was required to do.
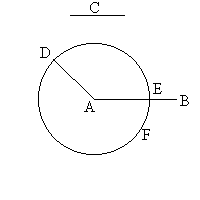
 We have already seen in an earlier essay that the Pythagoreans considered multiplication as the area of a rectangle. When they said "...the rectangle contained by two straight lines of length a and b..." they meant the area of the rectangle of sides a and b or the value of the product of a and b as opposite
We have already seen in an earlier essay that the Pythagoreans considered multiplication as the area of a rectangle. When they said "...the rectangle contained by two straight lines of length a and b..." they meant the area of the rectangle of sides a and b or the value of the product of a and b as opposite
 To divide a by c the Pythagoreans made a construction that was essentially to apply to the straight line of length c, a rectangle of area a. The width of the constructed rectangle would be the desired quotient.
To divide a by c the Pythagoreans made a construction that was essentially to apply to the straight line of length c, a rectangle of area a. The width of the constructed rectangle would be the desired quotient.
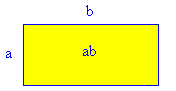
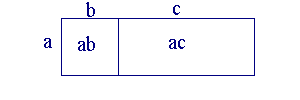 The Pythagoreans demonstrated this Law using the area of a rectangle of width a and length b+c, as in the diagram shown. The large rectangle is divided up into two smaller rectangles of size a by b and a by c respectively. The area of the large rectangle is a times (b + c). But the area of the larger rectangle is the sum of the areas of the two smaller ones or ab plus ac. So ab + ac = a(b+c).
The Pythagoreans demonstrated this Law using the area of a rectangle of width a and length b+c, as in the diagram shown. The large rectangle is divided up into two smaller rectangles of size a by b and a by c respectively. The area of the large rectangle is a times (b + c). But the area of the larger rectangle is the sum of the areas of the two smaller ones or ab plus ac. So ab + ac = a(b+c).
Proposition 3. If a straight line be cut at random, the rectangle contained by the whole and one of the segments is equal to the rectangle contained by the segments and the square on the aforesaid segment.
Proposition 4. If a straight line be cut at random, the square on the whole is equal to the squares on the segments and twice the rectangle contained by the segments.
Proposition 5 is discussed below. Interested readers can investigate others in Heath.
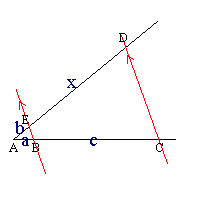 To solve the linear equation ax = bc, they used two properties which later appear as Propositions 8 and 9 in Book VI of The Elements. This involved making the construction opposite, the length x being the solution. The technique is based on the relationship a:b = c:x which results from the parallel lines EB and DC.
To solve the linear equation ax = bc, they used two properties which later appear as Propositions 8 and 9 in Book VI of The Elements. This involved making the construction opposite, the length x being the solution. The technique is based on the relationship a:b = c:x which results from the parallel lines EB and DC.
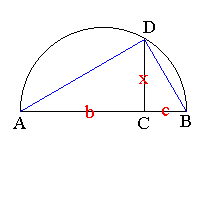 To solve the quadratic equation x2 = ab, they used what was to become Proposition 13 in Book VI of The Elements. This involved making the construction opposite, the length x being the solution. The technique is based on the relationship b:x = x:c which results from the properties of the similar triangles ACD and DCB. This process was also used to find the square root or to "square the rectangle".
To solve the quadratic equation x2 = ab, they used what was to become Proposition 13 in Book VI of The Elements. This involved making the construction opposite, the length x being the solution. The technique is based on the relationship b:x = x:c which results from the properties of the similar triangles ACD and DCB. This process was also used to find the square root or to "square the rectangle".
Solving Equations by Application of Areas
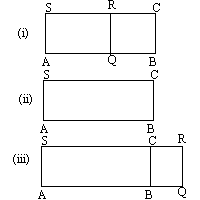 To appreciate application of areas, consider the rectangles ABCS and AQRS where the side AQ lies along the ray AB. When AQ is less than AB (i), the Pythagoreans would say that the rectangle AQRS is applied to segment AB, falling short by rectangle QBCR; when AQ is equal to AB (ii), they would say that the rectangle AQRS is applied to segment AB; when AQ is greater than AB (iii), they would say that the rectangle AQRS is applied to segment AB, exceeding by rectangle QBCR
To appreciate application of areas, consider the rectangles ABCS and AQRS where the side AQ lies along the ray AB. When AQ is less than AB (i), the Pythagoreans would say that the rectangle AQRS is applied to segment AB, falling short by rectangle QBCR; when AQ is equal to AB (ii), they would say that the rectangle AQRS is applied to segment AB; when AQ is greater than AB (iii), they would say that the rectangle AQRS is applied to segment AB, exceeding by rectangle QBCR
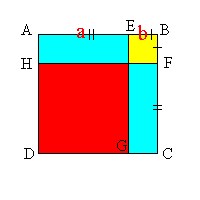
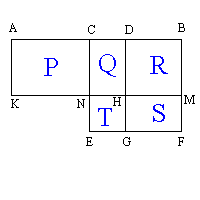 The diagram to demonstrate this is shown opposite. The straight line is AB, and it is cut equally at C and unequally at D. The rectangle ADHK is constructed where DH = DB. The square on CB and auxillary lines are also constructed. The proposition states that the area of the rectangle ADHK (P+Q) plus the area of the square NHGE (T) is equal to the area of the square CBFE (Q+R+S+T). I will leave it to the reader to establish this.
The diagram to demonstrate this is shown opposite. The straight line is AB, and it is cut equally at C and unequally at D. The rectangle ADHK is constructed where DH = DB. The square on CB and auxillary lines are also constructed. The proposition states that the area of the rectangle ADHK (P+Q) plus the area of the square NHGE (T) is equal to the area of the square CBFE (Q+R+S+T). I will leave it to the reader to establish this.
From the figure we can also establish that:
Now if we let the area of the said gnomon be b2 (say) and let AB = a, and DB = x then we can say that ax - x2 = b2. This is the quadratic x2 - ax + b2 = 0 .
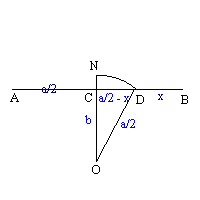 According to Heath the solution of ax - x2 = b2 was obtained with the construction "To a given straight line (a) to apply a rectangle which shall be equal to a given square (b2) and shall fall short by a square figure" as follows:
According to Heath the solution of ax - x2 = b2 was obtained with the construction "To a given straight line (a) to apply a rectangle which shall be equal to a given square (b2) and shall fall short by a square figure" as follows:
Hence, DB is found which equals x - one solution to the quadratic
ax - x2 = b2. The other solution being AD.
(a/2)2 = b2 + (a/2 - x)2
a2/4 = b2 + a2/4 - ax + x2
i.e. 0 = x2 - ax + b2
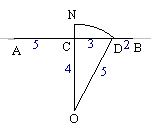 As an example let us solve x2 - 10x + 16 = 0
As an example let us solve x2 - 10x + 16 = 0
We start by drawing AB of length equal to 10 ( = a).
Next we bisect AB at C and construct the perpendicular CO of length equal to 4 (= b).
Draw the arc centre O of length equal to 5 ( = a/2) to cut AB at D.
Using triangle OCD and Pythagoras' theorem CD is of length 3.
The solution of the equation is x = 8 (AD) and x = 2 (DB).
You might like to do Activity 5 before you continue.
References: