Return to MENU
Back
PYTHAGORAS of SAMOS
A Collection of Essays and Lessons for Junior and Senior High School

Contents
13. A. Brief History of Geometry to the time of Pythagoras
14. B. The Postulational Method
15. C. The Regular Polygons and Polyhedrons
16. D. The Section
17. E. Transformation of Areas
18. Academic
Introduction:

In the three essays prior to this one, I outlined the influence of the Pythagoreans on Western science and philosophy, and in particular their contributions to mathematics in the areas of number theory and algebra. The interested reader will have recognised the significance of geometry in all these discoveries. This final essay on the Pythagoreans will attempt to describe some of their contributions to, and influence on, the body of geometry.

A. Brief History of Geometry to the time of Pythagoras

As has been discussed in the earlier essays, there are few surviving works from this period. Much of what follows is generally accepted as the history of geometry at this time.

The principal source of information concerning very early Greek geometry is the Eudemian Summary which is found in the introduction to Proclus' (500 A.D.) "Commentary of Euclid, Book I". Unfortunately the original reference, "The History of Geometry" by Eudemus (370 B.C.), who was a pupil of Aristotle, is lost. This book apparently gave a full account of the developments in geometry to about 335B.C. It is believed that Proclus had reference to it for his summary. What follows is from Proclus' summary of geometry up to Pythagoras as described in Allman[14]:

The Eudemian Summary attributes the origins of geometry to the Egyptians. It claims that the Egyptians invented geometry to restore the land boundaries which had been destroyed by the annual inundation of the Nile. Eudemus credits Thales of Miletus (ca. 640 - 548 B.C.) as having brought geometry into Greece :

"that he discovered many things himself, and communicated the beginnings of many to his successors, some of which he attempted in a more abstract manner and some in a more intuitional or sensible manner."

A review of available references to Thales credits him with the following geometrical results:

    (i) A circle is bisected by any diameter.
    (ii) The base angles of an isosceles triangle are equal.
    (iii) The vertical angles between two intersecting straight lines are equal.
    (iv) Two triangles are congruent if they have two angles and one side equal.
    (v) An angle in a semicircle is a right angle

Babylonian and Egyptian mathematics was basically "intuitional and sensible", there being little evidence to suggest that mathematics was valued as anything more than as an approximate, and useful tool for census, commerce, calendar construction, building and surveying. While Eudemus asserts that Thales discovered and transmitted many things in an "intuitional and sensible manner" he also credits Thales with making arguably the most important contribution to Western thought - the discovery (creation?) of the value of abstraction in proof. While rhetorical proof and concepts of truth had existed in some of the epic poetry of the times, such as in Homer's The Odyssey, Thales appears to be the first person in Western history to have valued logical, abstract discourse free of qualification.

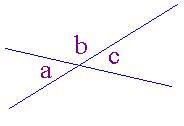One can only guess at the stimulus for such a revolutionary insight. It could possibly be that Thales' first glimpse of this idea occurred with the vertical angle theorem. That vertically opposite angles are congruent is easily demonstrated by folding about the intersecting point of both lines so that the two angles lay upon each other. The use of superposition to "prove" statements was a regular practice across the Middle East at this time.

Thales may have realised that this demonstration was only an illustration of one instance of the theorem, and that this theorem might be a "universal truth". Believing it to be a "universal truth" he might have looked for a general proof. It is possible that Thales' proof was similar to the one which is still used in mathematics classes today. In the figure above:

angle a plus angle b equals a straight line.
but angle c plus angle b equals a straight line.
so angle c must equal angle a.
Q.E.D.

The logical device used here was later recorded by Euclid [15] as common notion 1 in Book I of The Elements.

"1. Things that are equal to the same thing are also equal to one another."

Whether this was the first abstract proof or another was, the significant point is that the mathematical intellect was wakened. The secrets of the physical universe were exposed to clear analysis. This, or a similar proof, was the first abstract "truth", pure and immutable in a dusty, rhetorical and changing world. One can imagine that the human mind, released from the drudgery of everyday survival, (Thales was thought to be a wealthy merchant with ample leisure time) naturally seeks out and is seduced by the beauty and purity of abstraction.

This idea, that truth can only be sought in the purity of abstraction and therefore is mathematical in nature, was picked up and developed by Pythagoras and reached its zenith with Plato and Aristotle. The motto over the door to Plato's school The Academy was supposedly:

"Let no one unversed in geometry enter here".

The method which was developed over this time has become known as the Postulational Method. It is Aristotle who is credited with putting the final touches on the Postulational Method as it appears in The Elements.

After discussing Thales, Proclus next mentioned Ameristus for his "zeal in the study of geometry", and then claims:

"Then Pythagoras changed it into the form of a liberal science, regarding its principles in a purely abstract manner, and investigated its theorems from the immaterial and intellectual point of view…"

Thales was about 50 years senior to Pythagoras, and Miletus and Samos are very close geographically, so it may be that Pythagoras actually studied under Thales. Whether this was the case or not, most agree that Pythagoras was aware of, and built on the discoveries and teaching of Thales. It is also generally accepted that the Pythagoreans contributed the bulk of the first two books of The Elements (on angles, triangles, areas, and geometric algebra) together with some of books IV (polygons), VI (proportions) and XIII (polyhedrons).

Much of these have been loosely described in the earlier essays. What remains to be described is the development of the postulational method and some of the Pythagoreans more interesting geometrical discoveries.

B The Postulational Method

Eves [16] claims:

"Sometime between Thales in 600 B.C. and Euclid in 300 B.C., the notion was perfected of a logical discourse as a sequence of rigorous deductions from some initial and explicitly stated assumptions. This process, the so-called postulational method , has become the very core of modern mathematics; undoubtedly, much of the development of geometry along this pattern is due to the Pythagoreans."

The Postulational method (sometimes called the axiomatic or logico-deductive method) is shown in the diagram below.

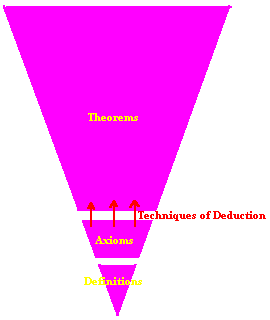
  • Initially a few key terms are introduced and defined.
  • Next some assumptions are declared which the reader is expected to accept without proof - these are called Postulates or Axioms.
  • All other facts and relationships, called theorems, are derived from these definitions and axioms using acceptable deductive processes.

Early Greek mathematicians and philosophers made a distinction between an axiom and a postulate. It is generally thought that there were three different distinctions made by the different groups at the time. Eves claims that Euclid considered an axiom as an "assumption common to all sciences", (the "common notions" in set A below) and a postulate as "an assumption peculiar to the particular science being studied", (set P below) as described in Book I of The Elements:

    A1. "Things which are equal to the same thing are also equal to one another.
    A2. "If equals be added to equals, the wholes are equal."
    A3. "If equals be subtracted from equals, the remainders are equal."
    A4. "Things which coincide with one another are equal to one another."
    A5. "The whole is greater that the part."
    P1. (It is possible) "to draw a straight line from any point to any other point."
    P2. (It is possible) "to produce a finite straight line continuously in a straight line."
    P3. (It is possible) "to describe a circle with any centre and distance."
    P4. (It is true) "that all right angles are equal to one another."
    P5. (It is true) "that, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles."

Building on the definitions, common notions, and postulates, the Pythagoreans were able to produce deductive proofs of a number of important geometric propositions (theorems). These axioms and proofs were further developed by several mathematicians up to Euclid, and have been a useful set of tools for many subsequent generations of mathematicians, showing how powerful and beneficial deductive reasoning can be! It would be misleading though, not to mention at this point, that there are considerable limitations of deductive reasoning in an axiomatic system; the major one being that any proof is only as good as the assumptions and axioms it starts off with! But it took nearly 2000 years after Pythagoras, before alternative geometries were found, ones that started from different assumptions and resulted in different propositions.

C. The Regular Polygons and Polyhedrons

"Polygon" is a Greek word meaning "many sides."The regular polygon is a convex plane shape (fills a flat surface) which has all of its sides the same length, and all its internal angles the same size. The simplest regular polygon is the equilateral triangle, then the square; following this, each polygon is named for the number of sides it possesses, the 5 sided pentagon, the 6 sided hexagon etc., as described in an earlier essay.

You might like to do Activity 6 and Activity 7 before you continue.

"Polyhedra" is a Greek word meaning "many faces." A regular polyhedron is a convex solid (fills space) that has all faces the same shape and size, and all internal angles between adjacent faces are the same. There are only 5 regular polyhedra - the 4 faced tetrahedron (the tetractys of a previous essay), 6 faced hexahedron (cube), 8 faced octahedron, 12 faced dodecahedron, and the 20 faced icosahedron as shown below.

Polyhedron Animator

  • Click on a buttons at left to see the solids.
  • Click on the solid to stop the rotation. Click to start again.

The regular polyhedra are commonly called the Platonic Solids because it is thought that Plato's Academy was the first to establish the geometrical methods to construct them (as in Book XIII of The Elements). It is generally accepted though that Pythagoras "produced" them and probably investigated some of their properties as in Allman:

"It is well known that the Pythagoreans were much occupied with the construction of regular polygons and solids, which in their cosmology played an essential part as the fundamental forms of the elements of the universe."

The interested reader should refer to an earlier essay which discusses the cosmological importance the Pythagoreans assigned to the regular solids.

It is thought that Pythagoras arrived at the regular polygons by investigating the properties of regular shapes which "filled the plane" around a point, and was probably influenced by the art of the day. Certainly the Babylonians and Egyptians had developed some ideas about the properties of tessellating shapes as evidenced in the tiling of their floors and walls etc. Also the presence of the crystalline shapes of pyrite and others was known at this time, and Heath claims that:

" It appears that dodecahedra have been found, of bronze or other material, which may belong to period's earlier than Pythagoras' time by some centuries."

The regular polygons (up to the hexagon) were constructed by the Pythagoreans with the use of inscribed circles as is represented in Books I and IV in "The Elements". In fact the very first Proposition (Book I Proposition 1) shows how to construct the equilateral triangle using congruent circles each intersecting the other's centre. The remaining constructions are generally those which also appear in mathematics text books today.

D. The Section

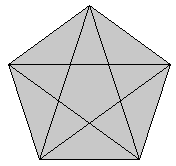If you join the vertices of the pentagon internally you arrive at the "star-pentagram" (opposite). The pentagram is claimed to have been the symbol of the Pythagorean Order and was given by them the name "HEALTH". As mentioned in an earlier essay, the pentagram is still claimed to have magical properties in modern mystic cults.

The construction of the regular pentagon is given in The Elements in Book IV Proposition 11. It makes use of the previous Proposition (10) to construct the "isosceles triangle whose base angles are twice the other", that is the 72-72-36 triangle. There are 10 such triangles in the figure opposite.

The construction of the triangle in Proposition IV. 10 relies on Proposition II. 11 which essentially divides a line in extreme and mean ratio, that is, the construction of the golden section. Heath claims that there is considerable justification for crediting the discovery of the section to the Pythagoreans considering that II. 11 is an example of application of areas which we have shown (in an earlier essay) to be Pythagorean. Johannes Kepler, in the sixteenth century claimed (in Boyer[17]):

"Geometry has two great treasures: one is the theorem of Pythagoras; the other, the division of a line into extreme and mean ratio. The first we may compare to a measure of gold; the second we may name a precious jewel"

E. Transformation of Areas

The Pythagoreans were interested in finding the area of any polygon. They did this by transforming the area of the given polygon into another plane shape whose area they could find, a square. To do this, they used what appears as Proposition 14 in Book II of The Elements, which in turn draws on II. 5, I. 42, I. 44, and I. 45 . To give an idea of their method Eves claims; "A simpler solution, probably also known to the Pythagoreans, is the following." He then describes the technique as set out below.

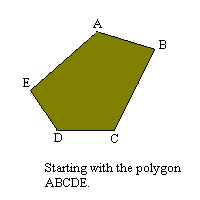Consider any polygon ABCDE (click several times on the diagram opposite). Draw BR parallel to AC to cut DC in R. Then, since triangles ABC and ARC have a common base (AC), and equal altitudes on this common base, these triangles have equal areas. It follows that polygons ABCDE and ARDE have equal areas. But the derived polygon has one less side than the given polygon. By a repetition of this process, we finally obtain a triangle (APR), having the same area as the given polygon. By dropping a perpendicular from one vertex (A) of the triangle to the opposite side (PR), they could use straightedge and compass to find the square whose area is congruent to the triangle.

Conclusion

In the previous four essays I have proposed that Western mathematics essentially began with the genius of Pythagoras. Where possible I have resisted the accounts of the more "romantic" versions of the achievements of Pythagoras and the Pythagoreans. There are some recent books on this theme, written for school students, which represents the man as a quaint mystic and follower of bizarre rituals. This is unfortunate, not only because it gives an historically inaccurate picture of the period, but also because the opportunity is lost to share with students the common bond (socially, culturally and intellectually) we have with this man and his ideas.

As the interested reader will already have noticed, the primary sources for these essays are about 100 years old. I am aware that there are more recent accounts of this period which credit Pythagoras with little more than forming shapes in the sand with pebbles. In these essays I have preferred to tell the more traditional version, in so doing I too may have succumbed to the romantic, but even so, I trust that this version has been worthy of the telling, and that it has provoked some reflection on the part of the interested reader.

Readers who would like to read more on the classical sources for our knowledge on Pythagoras, should look at the two essays at MacTutor - "How do we know about Greek Mathematics" and "How do we know about Greek Mathematicians".

References:

[14] Allman, George J., -Greek Geometry from Thales to Euclid , Dublin University Press 1877 (also on-line at "http://moa.cit.cornell.edu")

[15] Heath, Sir Thomas L., Euclid - The Thirteen Books of The Elements Second Edition, N.Y.: Dover Publications (orig 1908) - online with java applets. Another on-line version with java applets

[16] Eves, Howard, An Introduction To The History of Mathematics 5th Ed., N.Y.: Saunders College Publishing, 1983

[17] Boyer, Carl B., A History of Mathematics, N.Y.: John Wiley and Sons, 1968

This Essay and the related classroom Activities are on-line at MATHGYM ( http://www.mathtrak.com.au/mic/ )