Back
Activity 2 - Mathematical Method
This Activity and the related Essay on Pythagoras' Life are on-line at MATHGYM ( http://www.mathtrak.com.au/mic/ )In this activity you will investigate probably the most famous Mathematical equation in the world. You will also gain an insight into the way that Mathematicians work, and how they can be confident that their discoveries are right.
- INTRODUCTION - the Mathematics Method:
-
Mathematics is a very creative activity. Mathematicians who are also musicians, authors, and artists often talk about the creative similarities between Mathematics and the arts. Where Mathematics differs from the arts though, is that at its heart, it is a verifiable activity. By this I mean that Mathematics is interested in creating new ways of viewing the Universe that can be verified and accepted by others.
The challenge for Mathematicians is firstly to investigate some idea or part of the Universe which intrigues them, trying to find if there is some underlying pattern or structure. If the investigation reveals a pattern then an attempt is made to generalise about the pattern - this is called making a conjecture. (This is similar to a scientist formulating an hypothesis from observation.) The Mathematician then goes about trying to prove that the conjecture is correct. (This is slightly different from science which attempts to falsify the hypothesis - science accepts only those hypotheses which can be tested). In science an hypothesis is accepted, and lasts in use until it is falsified. In Mathematics, a conjecture is not accepted until its proof is established. If the conjecture is found to be false then we say the conjecture is refuted.
This process of Investigate -> Make a Conjecture-> Prove or Refute is what I mean by the Mathematical Method. In this Activity you will be expected to use the Mathematical Method to prove the most famous equation in the world.
- PART 1
-
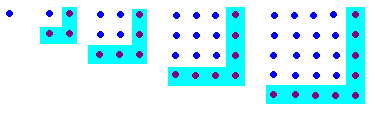
It really helps if you can get about 60 beads, or buttons or stones together for this part. Look at Figure 1 below. It represents the first five square numbers: 1, 4, 9, 16, 25. Square numbers are those numbers that are made by squaring any number. For example 9 is a square number because 32 = 9.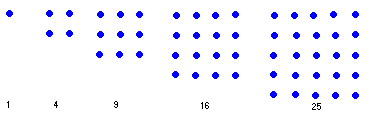
Figure 1
Figure 1 shows a special way of looking at square numbers. If you get some beads or stones you can make the square numbers by placing them in a square shape. In Figure 1 the first square number, ( 1 ) is made by simply placing 1 bead on a table; the second square number, ( 4 ) is made by placing 4 beads in a 2x2 square shape; the third square number, ( 9 ) is made by placing 9 beads in a 3x3 square shape and so on.Now let us clear the table and start all over again. Place a bead on the table to make the first square number.

Question 1: How can you add another three beads to make the second shape?
Question 2: How many beads do you need to add in the next gnomon to make the third shape from the second shape?
Question 3: Write down the number of beads needed in each of in the first 4 gnomon. What name do we give to the set of numbers that make up the gnomon?
Question 4: Do you think that all gnomon are odd numbers? This is a Conjecture. Write down what your conjecture is.
Let us pause for a while and think about what we have been doing. We have been Investigating some properties of square numbers, and now we have just made a Conjecture.
Question 5: Is the fact that "the difference between the first 5 consecutive square numbers is always odd" a proof of the Conjecture?
Proving the conjecture
Question 6: Can you use Figure 1 to prove this Conjecture?
Question 7: Complete the table below which shows each consecutive square number and gnomon. The first row has the number of the square number, the second row has the square number and the third row shows the difference between each square number (gnomon).Counting
Numbers1 2 3 4 5 6 7 8 9 10 11 12 13 14 Squares 1 4 9 16 25 \ / \ / \ / \ / \ / \ / \ / \ / / \ / \ / \ / \ / \ gnomon 3 5 7 9
Question 8: Circle any square numbers in the gnomon row. Make an arithmetic sum to show that the sum of a square number and a square number gnomon equals the next consecutive square number. I have written the first one down:
16 + 9 = 25 or 42 + 32 = 52 Do the same thing for the other sum in the table.
- PART 2
-
This relationship ( a2 + b2 = c2) has an interesting connection with right-angled triangles. Look at the right angled triangle below ( in yellow). The longest side (opposite the right angle) is called the hypotenuse. In the diagram, the hypotenuse is c and is 5 cm long. The length of the shortest side ( a ) is 3 cm, and the length of the remaining side ( b ) is 4 cm. Also notice that on each side of the triangle a square is drawn.
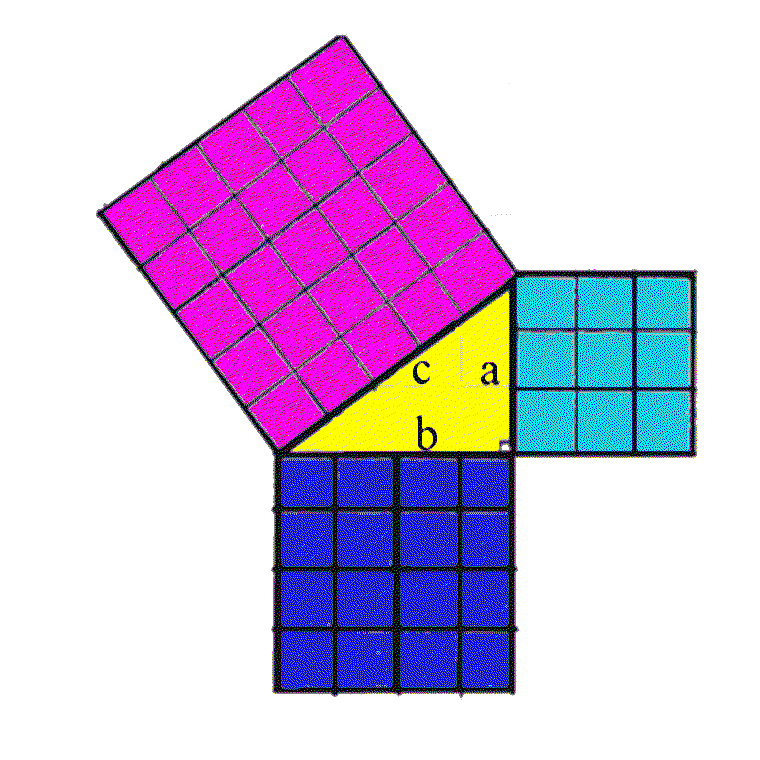
Question 9: Do you notice any relationship involving the addition of areas? Do you have a conjecture? Write a sentence describing your conjecture about the relationship and then write it as an equation in terms of a, b, and c
You might like to test your conjecture with the 5, 12, 13 relationship we found in Question 8 in addition to the 3, 4, 5 relationship.
Question 10: We have not proven our conjecture even though it seems to work when we test it. Why not?
Proving the conjecture
- Press "Start" button.
- Then follow the instructions clicking on and dragging the red dots and pressing the "next" button.
Since the 4 triangles have only changed their position, their areas haven't changed. So this means that the 2 visible blue squares must be the same area as the original internal blue square.
Question 11: Can you see from the two diagrams below that a2 + b2 = c2?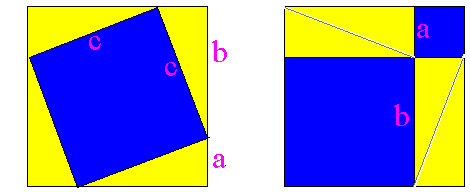
Question 11 - Answer
Now, how can we use this demonstration to write our proof ?
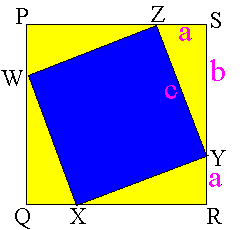
The first thing to establish is that WXYZ is a square. To do this we need to establish that :
- all sides are equal in length
- any one angle is right
Question 12: Can you establish these?
Question 13: What is the area of each of:- the square WXYZ,
- the square PQRS, and
- the total of the four triangles XRY+YSZ+ZPW+WQX?
Question 14: Can you now use these answers (from Question 13) to establish that a2 + b2 = c2?
This relationship a2 + b2 = c2, has been known and used in surveying since at least 1900 B.C.E., and yet we believe that it wasn't until he 6th century B.C.E. that the first proof was proposed by Pythagoras of Samos. For this reason the equation is called Pythagoras' Theorem .
Answer Question 1
I think I would answer Question 1 by placing the three beads in the "L" shape as highlighted in the diagram. In the centuries B.C.E. (Before the Christian Era) this "L" shape was called a gnomon (it resembles the oblique staff, which has the same name, used in sundials ).

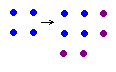
Answer Question 2
Did you get 5?
Answer Question 3
Did you get 3, 5, 7, 9 and did you say that these are odd numbers?
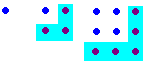
Answer Question 4
Did you say yes?
Here is my Conjecture.
The difference between consecutive square numbers is always odd.
Answer Question 5
No. A few examples may help us see a trend but even if we tried successfully for the first million square numbers we still couldn't be certain if the next one would work, or the one after that.
Answer Question 6
Here is my attempt.
By definition, every square number can be represented by a shape made up of beads which has the same number of rows as columns (e.g. the second figure, square number 4, has 2 rows of beads and two columns of beads). To make the next square number, ( e.g. 9 ) one extra bead is added to each row on the right and an one extra bead is added to each column at the bottom. Since the number of rows and columns are equal, an even number of beads has been added so far (e.g. 2+2 = 4 have been added to the 2x2 square).
Therefore, consecutive square numbers differ by an odd number. QED
Answer Question 7
| Counting Numbers | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Squares | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 |
| \ | / \ | / \ | / \ | / \ | / \ | / \ | / \ | / \ | / \ | / \ | / \ | / \ | / | |
| gnomon | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 |
Answer Question 8
Answer Question 9
The areas of the triangle are related: 9 + 16 = 25 or 32 + 42 = 52.
My conjecture is :
For a right angled triangle the sum of the squares on the two smaller sides is equal to the sum of the square on the hypotenuse - or a2 + b2 = c2.
Answer Question 10
Because specific cases do not prove for every case. We need to find a general proof, one that works for all right angled triangles.
Answer Question 11
The sides of the internal yellow square in Shape 1 are each c so the area is c2. The sides of the smaller yellow square in Shape 2 are a so the area is a2. Similarly the area of the larger square in Shape 2 is b2. Since the two yellow regions in both Shapes are the same area then a2 + b2 = c2

| Shape 1 | Shape 2 |
Answer Question 12

Angle XYR and angle ZYS add to 90 so angle XYZ must be 90 degrees, so the second condition is established.
Answer Question 13

- Area of square WXYZ is c2
- Area of square PQRS is (a+b)2 = (a+b)(a+b) = a2+2ab+b2
- Total Area of the triangles is 2ab
Answer Question 14

The Area of WXYZ = Area of PQRS - Area of the triangles
That is c2 = a2+2ab+b2 - 2ab
So c2 = a2+b2
QED